Next: 5 Photoionization modeling Up: Observations and three-dimensional photoionization Previous: 3 Kinematics
The derived electron temperatures (![]() ) and densities (
) and densities (![]() ) are listed in Table 5, together with the ionization potential required to create the emitting ions.
We obtained
) are listed in Table 5, together with the ionization potential required to create the emitting ions.
We obtained ![]() and
and ![]() from temperature-sensitive and density-sensitive emission lines by solving the equilibrium equations of level populations for a multilevel atomic model using EQUIB code (Howarth & Adams, 1981). The atomic data sets used for our plasma diagnostics from collisionally excited lines (CELs), as well as for abundances derived from CELs, are given in Table 4. The diagnostics procedure to determine temperatures and densities from CELs is as follows: we assume a representative initial electron temperature of 10000K in order to derive
from temperature-sensitive and density-sensitive emission lines by solving the equilibrium equations of level populations for a multilevel atomic model using EQUIB code (Howarth & Adams, 1981). The atomic data sets used for our plasma diagnostics from collisionally excited lines (CELs), as well as for abundances derived from CELs, are given in Table 4. The diagnostics procedure to determine temperatures and densities from CELs is as follows: we assume a representative initial electron temperature of 10000K in order to derive ![]() from
from ![]() S II
S II![]() line ratio; then
line ratio; then ![]() is derived from
is derived from ![]() N II
N II![]() line ratio in conjunction with the mean density derived from the previous step. The calculations are iterated to give self-consistent results for
line ratio in conjunction with the mean density derived from the previous step. The calculations are iterated to give self-consistent results for ![]() and
and ![]() . The correct choice of electron density and temperature is important for the abundance determination.
. The correct choice of electron density and temperature is important for the abundance determination.
We see that the PN Abell 48 has a mean temperature of
![]() N II
N II
![]() K, and a mean electron density of
K, and a mean electron density of
![]() S II
S II
![]() cm
cm![]() , which are in reasonable agreement with
, which are in reasonable agreement with
![]() N II
N II
![]() K and
K and
![]() S II
S II
![]() cm
cm![]() found by Todt et al. (2013). The uncertainty on
found by Todt et al. (2013). The uncertainty on
![]() N II
N II![]() is order of
is order of ![]() percent or more, due to the weak flux intensity of [N II]
percent or more, due to the weak flux intensity of [N II] ![]() 5755, the recombination contribution, and high interstellar extinction. Therefore, we adopted the mean electron temperature from our photoionization model for our CEL abundance analysis.
5755, the recombination contribution, and high interstellar extinction. Therefore, we adopted the mean electron temperature from our photoionization model for our CEL abundance analysis.
| Ion | Transition probabilities | Collision strengths |
|
N |
Bell et al. (1995) | Stafford et al. (1994) |
|
|
Zeippen (1987) | Pradhan et al. (2006) |
|
O |
Storey & Zeippen (2000) | Lennon & Burke (1994) |
|
|
Landi & Bhatia (2005) | McLaughlin & Bell (2000) |
|
|
Mendoza & Zeippen (1982) | Ramsbottom et al. (1996) |
|
S |
Mendoza & Zeippen (1982) | Tayal & Gupta (1999) |
| Huang (1985) | ||
|
|
Biémont & Hansen (1986) | Galavis et al. (1995) |
| Ion | Recombination coefficient | Case |
|
H |
Storey & Hummer (1995) | B |
|
|
Porter et al. (2013) | B |
|
|
Davey et al. (2000) | B |
Table 5 also lists the derived HeI temperatures, which are lower than the CEL temperatures, known as the ORL-CEL temperature discrepancy problem in PNe (see e.g. Liu et al., 2000; Liu et al., 2004b).
To determine the electron temperature from the HeI
![]() 5876, 6678 and 7281 lines, we used the emissivities of He I lines by Smits (1996), which also include the temperature range of
5876, 6678 and 7281 lines, we used the emissivities of He I lines by Smits (1996), which also include the temperature range of
![]() K. We derived electron temperatures of
K. We derived electron temperatures of
![]() K and
K and
![]() K from the flux ratio HeI
K from the flux ratio HeI
![]() 7281/5876 and
7281/5876 and
![]() 7281/6678, respectively. Similarly, we got
7281/6678, respectively. Similarly, we got
![]() K for HeI
K for HeI
![]() 7281/5876 and
7281/5876 and
![]() K for
K for
![]() 7281/6678 from the measured nebular spectrum by Todt et al. (2013).
7281/6678 from the measured nebular spectrum by Todt et al. (2013).
| Ion | Diagnostic | I.P.(eV) |
|
Ref. |
|
|
|
14.53 |
|
D13 |
|
|
T13 | |||
|
|
|
35.12 |
|
T13 |
| HeI |
|
24.59 |
|
D13 |
|
|
T13 | |||
| HeI |
|
24.59 |
|
D13 |
|
|
T13 | |||
|
|
||||
|
|
|
10.36 |
|
D13 |
|
|
T13 |
Using the effective recombination coefficients, we determine ionic abundances, X![]() /H
/H![]() , from the measured intensities of ORLs as follows:
, from the measured intensities of ORLs as follows:
Abundances of helium and carbon from ORLs are given in Table 6. We derived the ionic and total helium abundances from HeI ![]() 4471,
4471, ![]() 5876 and
5876 and ![]() 6678 lines. We assumed the Case B recombination for the HeI lines (Porter et al., 2013; Porter et al., 2012). We adopted an electron temperature of
6678 lines. We assumed the Case B recombination for the HeI lines (Porter et al., 2013; Porter et al., 2012). We adopted an electron temperature of
![]() K from HeI lines, and an electron density of
K from HeI lines, and an electron density of
![]() cm
cm![]() . We averaged the He
. We averaged the He![]() /H
/H![]() ionic abundances from the HeI
ionic abundances from the HeI ![]() 4471,
4471, ![]() 5876 and
5876 and ![]() 6678 lines with weights of 1:3:1, roughly the intrinsic intensity ratios of these three lines. The total He/H abundance ratio is obtained by simply taking the sum of He
6678 lines with weights of 1:3:1, roughly the intrinsic intensity ratios of these three lines. The total He/H abundance ratio is obtained by simply taking the sum of He![]() /H
/H![]() and He
and He![]() /H
/H![]() . However, He
. However, He![]() /H
/H![]() is equal to zero, since HeII
is equal to zero, since HeII ![]() 4686 is not present. The C
4686 is not present. The C![]() ionic abundance is obtained from C II
ionic abundance is obtained from C II ![]() 6462 and
6462 and ![]() 7236 lines.
7236 lines.
| Ion | Mult | Value
|
|
|
He |
4471.50 | V14 | 0.141 |
| 5876.66 | V11 | 0.121 | |
| 6678.16 | V46 | 0.115 | |
| Mean | 0.124 | ||
|
He |
4685.68 | 3.4 | 0.0 |
| He/H | 0.124 | ||
| C |
6461.95 | V17.40 | 3.068( |
| 7236.42 | V3 | 1.254( |
|
| Mean | 2.161( |
We determined abundances for ionic species of N, O, Ne, S and Ar from CELs. To deduce ionic abundances, we solve the statistical equilibrium equations for each ion using EQUIB code, giving level population and line sensitivities for specified
![]() cm
cm![]() and
and
![]() K adopted according to our photoionization modeling. Once
the equations for the population numbers are solved, the ionic abundances, X
K adopted according to our photoionization modeling. Once
the equations for the population numbers are solved, the ionic abundances, X![]() /H
/H![]() , can be derived from the observed line intensities of CELs as follows:
, can be derived from the observed line intensities of CELs as follows:
Total elemental and ionic abundances of nitrogen, oxygen, neon, sulfur and argon from CELs are presented in Table 7. Total elemental abundances are derived from ionic abundances using the ionization correction factors (![]() ) formulas given by Kingsburgh & Barlow (1994). The total O/H abundance ratio is obtained by simply taking the sum of the O
) formulas given by Kingsburgh & Barlow (1994). The total O/H abundance ratio is obtained by simply taking the sum of the O![]() /H
/H![]() derived from [O II]
derived from [O II]
![]() 3726,3729 doublet, and the O
3726,3729 doublet, and the O![]() /H
/H![]() derived from [O III]
derived from [O III]
![]() 4959,5007 doublet, since HeII
4959,5007 doublet, since HeII ![]() 4686 is not present, so O
4686 is not present, so O![]() /H
/H![]() is negligible.
The total N/H abundance ratio was calculated from the N
is negligible.
The total N/H abundance ratio was calculated from the N![]() /H
/H![]() ratio derived from the [N II]
ratio derived from the [N II]
![]() 6548,6584 doublet, correcting for the unseen N
6548,6584 doublet, correcting for the unseen N![]() /H
/H![]() using,
using,
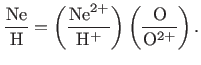 |
(4) |
![\includegraphics[width=1.7in]{figures/fig9_AbHeII.eps}](img265.png)
![\includegraphics[width=1.7in]{figures/fig9_AbNIICEL.eps}](img266.png) ![\includegraphics[width=1.7in]{figures/fig9_AbOIIICEL.eps}](img267.png) ![\includegraphics[width=1.7in]{figures/fig9_AbSIICEL.eps}](img268.png)
|
Fig.4 shows the spatial distribution of ionic abundance ratio He![]() /H
/H![]() , N
, N![]() /H
/H![]() , O
, O![]() /H
/H![]() and S
and S![]() /H
/H![]() derived for given
derived for given
![]() K and
K and
![]() cm
cm![]() . We notice that both O
. We notice that both O![]() /H
/H![]() and He
and He![]() /H
/H![]() are very high over the shell, whereas N
are very high over the shell, whereas N![]() /H
/H![]() and S
and S![]() /H
/H![]() are seen at the edges of the shell. It shows obvious results of the ionization sequence from the
highly inner ionized zones to the outer low ionized regions.
are seen at the edges of the shell. It shows obvious results of the ionization sequence from the
highly inner ionized zones to the outer low ionized regions.
| Ion | Mult | Value
|
|
|
N |
6548.10 | F1 | 1.356( |
| 6583.50 | F1 | 1.486( |
|
| Mean | 1.421( |
||
| 3.026 | |||
| N/H | 4.299( |
||
| O |
3727.43 | F1 | 5.251( |
|
O |
4958.91 | F1 | 1.024( |
| 5006.84 | F1 | 1.104( |
|
| Average | 1.064( |
||
| 1.0 | |||
| O/H | 1.589( |
||
| Ne |
3868.75 | F1 | 4.256( |
| 1.494 | |||
| Ne/H | 6.358( |
||
| S |
6716.44 | F2 | 4.058( |
| 6730.82 | F2 | 3.896( |
|
| Average | 3.977( |
||
|
S |
9068.60 | F1 | 5.579( |
| 1.126 | |||
| S/H | 6.732( |
||
| Ar |
7135.80 | F1 | 9.874( |
| 1.494 | |||
| Ar/H | 1.475( |
Ashkbiz Danehkar 2014-04-19